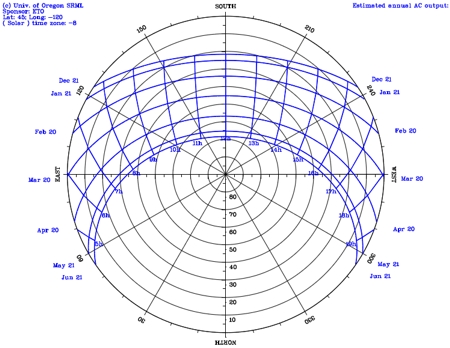
University of Oregon (SRML) 'Live' graphical display, updated every 60 seconds. 'Live' data and plots, updated every 60 seconds. Daily plots and raw data files, are available from August 19, 2016 to yesterday. Solar Calendars, are available from August 2016 to present month. SunPath is a little app that shows sun movement and sunlight phases during the given day at the given location. Want to know where the sun is for today's date and at the present moment for the selected location? Find Now Please scroll the yellow dot on the time bar above the map from left to right to see the exact sun path. Mar 05, 2007 Sun path chart program This program creates sun path charts in Cartesian coordinates for: (1) 'typical' dates of each month (i.e.; days receiving about the mean amount of solar radiation for a day in the given month); (2) dates spaced about 30 days apart, from one solstice to the next; or (3) a single date you specify. There is also the Sun path chart program that creates sun path charts in Cartesian coordinates for: (1) 'typical' dates of each month (i.e.; days receiving about the mean amount of solar radiation for a day in the given month); (2) dates spaced about 30 days apart, from one solstice to the next; or (3) a single date you specify.
Great Circles:To explore the solar system, one first needs a coordinate system, a map. For gettingaround town, a flat map works fine with four directions, north, east, south, west.However, the sky appears to look like a sphere, so spherical coordinates areneeded.
The shortest path between two points on a plane is a straight line. Onthe surface of a sphere, however, there are no straight lines. Theshortest path between two points on the surface of a sphere is given bythe arc of the great circle passing through the two points. A great circleis defined to be the intersection with a sphere of a plane containing thecenter of the sphere.
Two great circles
If the plane does not contain the center of the sphere, its intersectionwith the sphere is known as a small circle. In more everyday language, ifwe take an apple, assume it is a sphere, and cut it in half, we slicethrough a great circle. If we make a mistake, miss the center and hencecut the apple into two unequal parts, we will have sliced through a smallcircle.
Two small circles
Spherical Triangles:
If we wish to connect three points on a plane using the shortest possibleroute, we would draw straight lines and hence create a triangle. For asphere, the shortest distance between two points is a great circle. Byanalogy, if we wish to connect three points on the surface of a sphereusing the shortest possible route, we would draw arcs of great circles andhence create a spherical triangle. To avoid ambiguities, a triangle drawnon the surface of a sphere is only a spherical triangle if it has all ofthe following properties:
- The three sides are all arcs of great circles.
- Any two sides are together greater than the third side.
- The sum of the three angles is greater than 180°.
- Each spherical angle is less than 180°.
The figure below shows a spherical triangle, formed by three intersectinggreat circles, with arcs of length (a,b,c) and vertexangles of (A,B,C).
Note that the angle between two sides of a spherical triangle is definedas the angle between the tangents to the two great circle arcs, as shownin the figure below for vertex angle B.
Earth's Surface:
The rotation of the Earth on its axis presents us with an obvious means ofdefining a coordinate system for the surface of the Earth. The two pointswhere the rotation axis meets the surface of the Earth are known as thenorth pole and the south pole and the great circle perpendicular to therotation axis and lying half-way between the poles is known as theequator. Great circles which pass through the two poles are known asmeridians and small circles which lie parallel to the equator are known asparallels or latitude lines.
The latitude of a point is the angular distance north or south of theequator, measured along the meridian passing through the point. A relatedterm is the co-latitude, which is defined as the angular distance betweena point and the closest pole as measured along the meridian passingthrough the point. In other words, co-latitude = 90° - latitude.
Distance on the Earth's surface is usually measured in nautical miles,where one nautical mile is defined as the distance subtending an angle ofone minute of arc at the Earth's center. A speed of one nautical mile perhour is known as one knot and is the unit in which the speed of a boat oran aircraft is usually measured.
Horizon System:
Humans perceive in Euclidean space -> straight lines and planes.But, when distances are not visible (i.e. very large) than theapparent shape that the mind draws is a sphere -> thus, we use aspherical coordinate system for mapping the sky with the additionaladvantage that we can project Earth reference points (i.e. NorthPole, South Pole, equator) onto the sky. Note: the sky is not reallya sphere!
From the Earth's surface we envision a hemisphere and mark the compasspoints on the horizon. The circle that passes through the south point,north point and the point directly over head (zenith) is called themeridian.
This system allows one to indicate any position in the sky by tworeference points, the time from the meridian and the angle from thehorizon. Of course, since the Earth rotates, your coordinates willchange after a few minutes.
The horizontal coordinate system (commonly referred to as the alt-azsystem) is the simplest coordinate system as it is based on the observer'shorizon. The celestial hemisphere viewed by an observer on the Earth isshown in the figure below. The great circle through the zenith Z and thenorth celestial pole P cuts the horizon NESYW at the north point (N) andthe south point (S). The great circle WZE at right angles to the greatcircle NPZS cuts the horizon at the west point (W) and the east point (E).The arcs ZN, ZW, ZY, etc, are known as verticals.
The two numbers which specify the position of a star, X, in this systemare the azimuth, A, and the altitude, a. The altitude of X is the anglemeasured along the vertical circle through X from the horizon at Y to X.It is measured in degrees. An often-used alternative to altitude is thezenith distance, z, of X, indicated by ZX. Clearly, z = 90 - a. Azimuthmay be defined in a number of ways. For the purposes of this course,azimuth will be defined as the angle between the vertical through thenorth point and the vertical through the star at X, measured eastwardsfrom the north point along the horizon from 0 to 360°. This definitionapplies to observers in both the northern and the southern hemispheres.
It is often useful to know how high a star is above the horizon and inwhat direction it can be found - this is the main advantage of the alt-azsystem. The main disadvantage of the alt-az system is that it is a localcoordinate system - i.e. two observers at different points on the Earth'ssurface will measure different altitudes and azimuths for the same star atthe same time. In addition, an observer will find that the star's alt-azcoordinates changes with time as the celestial sphere appears to rotate.Despite these problems, most modern research telescopes use alt-az mounts,as shown in the figure above, owing to their lower cost and greater stability.This means that computer control systems which can transform alt-azcoordinates to equatorial coordinates are required.
Celestial Sphere:
The celestial sphere has a north and south celestial pole as well as acelestial equator which are projected reference points to the samepositions on the Earth surface. Right Ascension and Declination serve asan absolute coordinate system fixed on the sky, rather than a relativesystem like the zenith/horizon system. Right Ascension is the equivalentof longitude, only measured in hours, minutes and seconds (since the Earthrotates in the same units). Declination is the equivalent of latitudemeasured in degrees from the celestial equator (0 to 90). Any point ofthe celestial (i.e. the position of a star or planet) can be referencedwith a unique Right Ascension and Declination.
The celestial sphere has a north and south celestial pole as well as acelestial equator which are projected from reference points from the Earthsurface. Since the Earth turns on its axis once every 24 hours, the starstrace arcs through the sky parallel to the celestial equator. Theappearance of this motion will vary depending on where you are located onthe Earth's surface.
Note that the daily rotation of the Earth causeseach star and planet to make a daily circular path around the northcelestial pole referred to as the diurnal motion.
Equatorial Coordinate System :
Because the altitude and azimuth of a star are constantly changing, it isnot possible to use the horizontal coordinate system in a catalog ofpositions. A more convenient coordinate system for cataloging purposes isone based on the celestial equator and the celestial poles and defined ina similar manner to latitude and longitude on the surface of the Earth. Inthis system, known as the equatorial coordinate system, the analog oflatitude is the declination, δ.The declination of a star is its angular distance in degrees measured fromthe celestial equator along the meridian through the star. It is measurednorth and south of the celestial equator and ranges from 0° at thecelestial equator to 90° at the celestial poles, being taken to be positivewhen north of the celestial equator and negative when south. In the figure below,the declination of the star X is given by the angle between Y and X.
The analog of longitude in the equatorial system is the hour angle, H(you may also see the symbol HA used). Defining the observer's meridianas the arc of the great circle which passes from the north celestial polethrough the zenith to the south celestial pole, the hour angle of a staris measured from the observer's meridian westwards (for both northern andsouthern hemisphere observers) to the meridian through the star (from 0° to360°). Because of the rotation of the Earth, hour angle increases uniformlywith time, going from 0° to 360° in 24 hours. The hour angle of a particularobject is therefore a measure of the time since it crossed the observer'smeridian - hence the name. For this reason it is often measured in hours,minutes and seconds of time rather than in angular measure (just likelongitude). In figure above, the hour angle of the star X is given by theangle Z-NCP-X. Note that all stars attain their maximum altitude above thehorizon when they transit (or attain upper culmination on, in the case ofcircumpolar stars) the observers meridian.
The declination of a star does not change with time. The hour angle does,and hence it is not a suitable coordinate for a catalogue. This problem isovercome in a manner analogous to the way in which the Greenwich meridianhas been (arbitrarily) selected as the zero point for the measurement oflongitude. The zero point chosen on the celestial sphere is the firstpoint of Aries, γ, and theangle between it and the intersection of the meridian through a celestialobject and the celestial equator is called the right ascension (RA) of theobject. Right ascension is sometimes denoted by the Greek letter αand is measured from 0h to24h along the celestial equator eastwards (in the direction of aright-handed screw motion about the direction to the north celestial pole)from the first point of Aries, that is, in the opposite direction to thatin which hour angle is measured. Like the definition of hour angle, thisconvention holds for observers in both northern and southern hemispheres.In above figure, the right ascension of the star X is given by the angle-NCP-Y.
Most modern research telescopes do not use equatorial mounts due to theirhigher cost and lower stability. This is at the expense of the simplicityof telescope tracking - an equatorially-mounted telescope need only moveits right ascension axis in order to track the motion of the celestialsphere. The figure above shows an example of an equatorially-mountedtelescope.
The above diagram displays the typical motion of a star or planet in the sky, withthe relevant angles marked. The star, X, crosses the horizon at L and V, travelingfrom L through U on the meridian, down to V. H is the hour angle of the star, whichwill equal the arc BT, but not the arc XU.Constellations:
Drawn onto the celestial sphere are imaginary shapes calledconstellations, Latin for `group of stars'. Due to the nature of the Earth'ssurface, the sky is divided into the northern and southern sky as seen from eachhemisphere.
Northern SkySouthern SkyConstellations are oftendrawn in the shapes of mythical heros and creatures tracing a pattern ofstars on the celestial sphere, recorded on a star map.The origin of the names of particular constellations is lost with time,dating back before written records. The ancient Greeks were the first torecord the oral legends. But the boundaries of the constellations werefixed by the International Astronomical Union in 1928. For many of theconstellations it is easy to see where they got their names. For example,
University Of Portland
Aquila, the EagleHercules, the WarriorScorpius, the ScorpionIn all, there are 88 constellationnames cataloged by Hipparchus in 100 B.C. To find out more about yourfavorite constellation, goto Constellationof the Month. Since the boundaries are fixed, a star will always remain in aconstellation unless its proper motion moves it into another.
Star Names:
August 18, 2016 - This PAR has been reissued as PAR-16-413.; NOT-OD-16-004 - NIH & AHRQ Announce Upcoming Changes to Policies, Instructions and Forms for 2016 Grant Applications (November 18, 2015); NOT-OD-16-006 - Simplification of the Vertebrate Animals Section of NIH Grant Applications and Contract Proposals (November 18, 2015); NOT-OD-16-011 - Implementing Rigor and Transparency in. Par 13. Applications to implement definitive efficacy trials (e.g., Phase 3 trials of drugs or Pivotal device trials) should be submitted to PAR-13-278, NINDS Investigator-Initiated Phase 3 Clinical Trials. June 24, 2015 - This PA has been reissued as PAR-15-287.; August 18, 2014 - See Notice NOT-LM-14-004.Updated to include NLM's participation in this PAR. May 9, 2014 - Notice of Change in Eligibility for PAR-13-358. See Notice NOT-HD-14-015. January 17, 2014. Part 13—Simplified Acquisition Procedures. 13.000 Scope of part. 13.001 Definitions. 13.004 Legal effect of quotations. 13.005 List of laws inapplicable to contracts and subcontracts at or below the simplified acquisition threshold. 13.006 Inapplicable provisions and clauses. Subpart 13.1—Procedures. February 19, 2016 - This PAR has been reissued as PAR-16-103.; June 4, 2014 - Notice NOT-14-074 supersedes instructions in Section III.3 regarding applications that are essentially the same.; November 27, 2013 (NOT-OD-14-027) - NIH to Require Use of Updated Electronic Application Forms for Due Dates on or after January 25, 2014.Forms-C applications are required for due dates on or after.
Hipparchus also developed a simply method of identifying the stars in thesky by using a letter from the Greek alphabet combined with theconstellation name.
So, for example, the brightest star in the constellation Orion is AlphaOrion, the second brightest star is Beta Orion, and so on. When theletters run out, we use a number 33 Orion, 101 Orion, etc. Some of thevery brightest stars have their own names due to their importance to earlynavigators. For example, Alpha Canis Major is Sirius, the Dog Star.
About 6000 stars are visible with the naked eye on a dark, moonlessnight. However, there are over 1013 stars in the whole MilkyWay galaxy were the solar system resides. Thus, we only see a very smallfraction of the closest and brightest stars with our eyes. The first star catalogwas published by Ptolemy in the 2nd century. It contained the positions of 1025 ofthe brightest stars in the sky. The first modern star catalog was the BonnerDurchmusterung by Argelander in 1860, containing 320,000 stars.
Since the Earth's axis is tilted 23 1/2 degrees from the plane of ourorbit around the Sun, The apparent motion of the Sun through the skyduring the year is a circle that is inclined 23 1/2 degrees from thecelestial equator. This circle is called the ecliptic and passesthrough 12 of the 88 constellations that we call the zodiac.
Equinox and Solstice:
The projection of the Sun's path across the sky during the year iscalled the ecliptic. The points where the ecliptic crosses thecelestial equator are the vernal and autumnal equinox's. The pointwere the Sun is highest in the northern hemisphere is called thesummer solstice. The lowest point is the winter solstice.
Days are longest in the summer for the northern hemisphere due to tiltof the Earth's axis allowing for more sunlight to be projected ontosurface. Note also the reason for the 'midnight' sun at the North Polein summer. Longest day of the year is at the summer solstice
For opposite reasons, days are short and nights long in the winter.
Seasons:
The seasons are caused by the angle the sun's rays make with the ground.Higher Sun angle means more luminosity per square meter. Low Sun angleproduces fewer rays per square meter. More intensity means more heat and,therefore, higher temperatures.
Note that, due to the fact that our oceans store heat, the actual changesin mean Earth temperature are delayed by several weeks, i.e. the hottestdays of summer are usually in late July, over a month from the summersolstice.
Sidereal and Synodic time:
A `day' is defined by the rotation of object in question. For example,the Moon's `day' is 27 Earth days.
A `year' is defined by the revolution of object in question. Forexample, the Earth's year is 365 days divided into months; whereas, Pluto's `year' is 248.6 Earthyears.
Typical we use synodic time, which means with respect to the Sun, inour everyday life. For example, noon, midnight, twilight are allexamples of synodic time based on where the Sun is in the sky (e.g.directly overhead on the equator for noon). Astronomers often usesidereal time, which means time with respect to the stars, for theirmeasurements.
Since the Earth moves around the Sun once every 365 days, the Sun'sapparent position in the sky changes from day to day.
University Of Washington
Note, in the above diagram, we see that the Earth's synodic day is 4mins longer than its sidereal day.Phases of the Moon:
University Of Oregon Sun Path Chart
The Moon is tidally locked to the Earth, meaning that one side alwaysfaces us (the nearside), whereas the farside is forever hidden from us.In addition, the Moon is illuminated on one side by the Sun, the otherside is dark (night).
Which parts are illuminated (daytime) and which parts we see from theEarth are determined by the Moon's orbit around the Earth, what is calledthe phase of the Moon (click here for the currentphase of the Moon).
University Of Oregon Sun Path
As the Moon moves counterclockwise around the Earth, the daylight sidebecomes more and more visible (i.e. we say the Moon is `waxing'). After full Moon isreached we begin to see more and more of the nighttime side (i.e. we saythe Moon is `waning'). This whole monthly sequence is called the phases of the Moon.
Eclipses:
University Of Oregon Sun Path Chart
On rare occasions the Moon comes between the Earth and the Sun (a solar eclipse) or the Moonenters the Earth's shadow (a lunar eclipse).
University Of Oregon Sun Path
Eclipses only occur when the line of nodes is aligned with the Sun (2to 5 times a year). All solar eclipses occur at new moon with a duration of only 4 to 7 mins.The path of shadow across surface of the Earth determines who gets to seeit.All lunar eclipses occur at full moon and everyone on nightside of Earthis able to observe lunar eclipses. The deep red color during the eclipsecomes from light refracted through Earth's atmosphere (i.e. redsunset's)